Banach-Tarski: weird triangles
Okay, this has nothing to do with Banach-Tarski mathematically, but it is disturbing and unsettling for exactly the same reasons. Alert reader Brian sent me this image of cut-up and reassembled triangles. See if you can figure out what's going on.
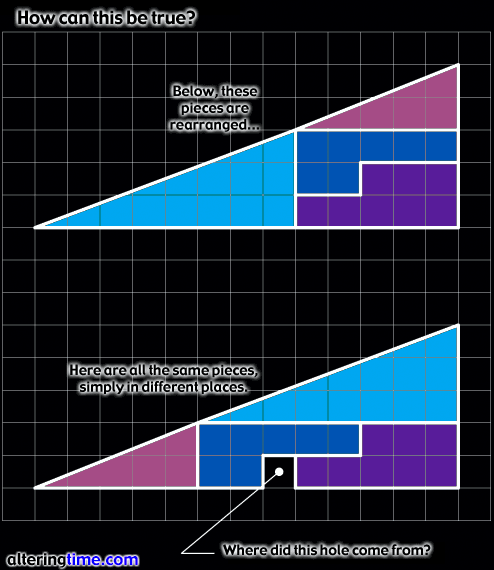
Comments
damn i just blew 10 minutes on that and i got nuthin to show for it.
Posted by: ortho | March 27, 2006 07:53 PM
That looks like a poor Tetris strategy.
Posted by: CRB | March 27, 2006 08:46 PM
Thats interesting. I am not sure I figured it correctly, but I believe that the hole is also present in the 3-dimensional structure of the top triangle, and after the rearrangements it can be simply seen in the lateral surface. Is that it?
Posted by: Blue Wind | March 27, 2006 09:50 PM
Hint: Calculate the areas.
Posted by: PR | March 27, 2006 10:17 PM
I'm no math major, but I would guess that if the areas of the triangles in the two examples are different then it could certainly explain the hole.
Posted by: Al D. | March 27, 2006 10:43 PM
However the area of the two triangles are the same in both examples... They are identical.
Posted by: PR | March 27, 2006 10:50 PM
PR,
I think it is what I wrote above. The hole must exist in the 3-dimensional structure of the first triangle, and after the rearrangements it can be seen in the lateral surface. What we see in the picture is one dimension only.
Posted by: Blue Wind | March 28, 2006 07:28 AM
Some tips: You can assume that all the pieces are indeed exactly the same size and shape in the two different configurations, and also they are all strictly two-dimensional, not 2D projections of a 3D object.
Posted by: BNJ | March 28, 2006 08:43 AM
OK. I am officially stumped.
Posted by: Adam | March 28, 2006 09:21 AM
Yet more math blogging?! Did you not realize that I was kidding when I mentioned my finely honed Asian math mind? I was an ENGLISH major! :P
Posted by: K | March 28, 2006 09:24 AM
I'm afraid my geometry skills are a little rusty, but are either of the two figures actually triangles?
The hypotenuse of the pink triangle has a slope of 5/2 while the hypotenuse of the blue triangle has a slope of 8/3.
I think this is basically an optical illusion!
Posted by: withoutfeathers | March 28, 2006 09:59 AM
Ok, I think I finally got it. If you calculate the surfaces they are both the same. The extra space for the hole in the second triangle is distributed to other areas at the periphery that are optically impossible to appreciate at first glance. But there are clear-cut differences. The best place to appreciate the differences is probably in the 4th column from the left. In the bottom triangle there is more space occupied in the very top square than in the top triangle. Pfeeww..
Posted by: Blue Wind | March 28, 2006 10:21 AM
Actually, I meant the best place to appreciate the differences is the 4th column from the right.
Posted by: Blue Wind | March 28, 2006 10:23 AM
WF - and the big triangle has a slope of 13/5. Not much of a difference with that pesky white line there.
Good thing to remember next time I publish a prospectus.
Posted by: PR | March 28, 2006 10:39 AM
"WF - and the big triangle has a slope of 13/5. Not much of a difference with that pesky white line there."
Actually, I'm saying that I don't think there are any "big" triangles in the illustration. Just two small triangles (blue and pink) arranged with other geometric shapes to give the illusion of big "triangles."
Posted by: withoutfeathers | March 28, 2006 10:57 AM
WF,
You are almost as wrong as you were when you thought Saddam Hussein had WMDs. Read what I wrote. I am pretty confident that's the answer.
Posted by: Blue Wind | March 28, 2006 11:30 AM
When did I think Saddam had WMD?
I always assumed Bill Clinton and Hans Blix were lying about that.
Posted by: withoutfeathers | March 28, 2006 11:36 AM
The assemblage of four shapes does not make a triangle. They make a rhombus with four sides and four angles. This can be seen when you find the length of the two triangles' hypoteni. The pink triangle has a hypotenuse of 5.385164807134504. The hypotenuse of the light blue triangle is 8.54400374531753. If you add those two up you get 17.08800749063506. If the assemblage was in fact a triangle you would expect this to be the hypotenuse of the whole triangle but in reality, 13^2+5^2 is 194 and the square root of 194 is 13.92838827718412 not 17.08800749063506. With the thick white line it’s hard to tell but the two “diagonal line” (underneath the handy bold lettering) is bent in both pictures out in the one missing the space and in with the one with the extra space.
Posted by: Peter | March 28, 2006 12:24 PM
Man, if the answer to this comes down to miniscule differences in hypotenuse lengths and bent white-line thicknesses i am gonna be so pissed off.
Posted by: ortho | March 28, 2006 12:47 PM
We're on the same page... Except for I think the BW 3D thing is off the deep end. I haven't followed his posts but I'd bet he's a conspiracy thinker.
When I said the "big triangle" I meant the shape as it appears. Here's a pseudo-proof:
The area of the big apparent triangle is 5*13/2 = 32.5.
The area of the pieces are pink=2*5/2=5, blue=3*8/2=12, and 15 for the rectangles. Total of pieces = 32.
The difference is 0.5, which is the area of the tiny triangle that bows inward from the imaginary hypotenuse and the real hypotenuses. In the bottom example, it's the same bowed outward, also with area 0.5.
The difference is 0.5+0.5=1. Not quite QED, but something like that....
Posted by: PR | March 28, 2006 01:49 PM
Except for I think the BW 3D thing is off the deep end....I'd bet he's a conspiracy thinker.
Well the 3D thing was a possibility if we were talking about 3-dimensional structures. But after Barry clarified, I gave an explanation similar to what you gave, albeit less detailed. Take a look. So if I am a conspiracy thinker, you may also be one and you dont know it :)
Posted by: Blue Wind | March 28, 2006 02:03 PM
Just kidding! Now I'm going to have to go check to see if I'm a conspiracy thinker too.
Posted by: PR | March 28, 2006 02:08 PM
"But after Barry clarified, I gave an explanation similar to what you gave, albeit less detailed. Take a look."
Ummm...actually BW, you changed your tune after I suggested that this was "basically an optical illusion."
22 minutes later you declared that it was: "...optically impossible to appreciate at first glance..." and then tried to tie me to Saddam Hussein's WMD!
This is a consipiracy if I ever smelled one!
Posted by: withoutfeathers | March 28, 2006 04:27 PM
WF,
Sorry but if you read carefully you will realize that were you talking about "optical illusions" without any substantiation of coherent meaning. You almost sounded like "president" Bush :)
Posted by: Blue Wind | March 28, 2006 05:06 PM
"Sorry but if you read carefully you will realize that were you talking about "optical illusions" without any substantiation of coherent meaning."
Actually I pointed out that the two "big" triangles couldn't, in fact, be triangles because the two segments of the hypotenus did not have equivalent slopes.
All you did was speculate about the "surface areas" of the two "triangles" which, in fact, are not triangles at all.
You almost sounded like John Kerry remeniscing about Christmas Day in Cambodia.
Posted by: withoutfeathers | March 28, 2006 05:23 PM
What does that make me, Karl Rove? Cato Institute?
There has to be a place for a perhaps-conspiracy theorist, who somehow doesn't know he's a conspiracy theorist, but has all of the data to back it up...
Posted by: PR | March 28, 2006 05:36 PM
I think I've found the "hole" in the top triangle.
First calculate the areas of each component shape:
Lt Blue = 12
Pink = 5
Dk Blue = 7
Purple = 8
TOTAL = 32
Now calculate the area of the completed triangle (top picture):
13 * 5 / 2 = 32.5
Voila.
Posted by: CRB | March 28, 2006 09:52 PM
CRB,
Too late. WF believes he found it first (the same way that Bush believes he is winning the war in Iraq).
Posted by: Blue Wind | March 28, 2006 10:04 PM
No Blue Wind, I don't believe I found the answer first. I was the first to suggest that the two major figures were not actually triangles. Peter was the first to provide a mathematical explanation, although I believe PR's explanation was equally correct -- and perhaps more elegant.
Have to give CRB style points, however for the most transparent explanation.
And I still think Bill Clinton and Hans Blix were lying when they said Hussein had WMD.
Posted by: withoutfeathers | March 28, 2006 10:57 PM
Heck, maybe the WMD are in that unit of missing area in the puzzle. The WMD *were* there in the bottom diagram, but now where are they? Syria?
Posted by: PR | March 28, 2006 11:08 PM
Oops, I didn't refresh the comments page before posting last night, so I missed the exchange between wf, peter and PR.
Well done and sorry for my redundancy.
Posted by: CRB | March 29, 2006 10:19 AM
WF,
You are almost as wrong as you were when you thought Saddam Hussein had WMDs. Read what I wrote. I am pretty confident that's the answer.
LOL, that explains a lot Blue Wind. ;-)
Posted by: CRB | March 29, 2006 10:24 AM
Just to clarify my post above, triangle should have been in quotes as the top picture is a quadrilateral while the bottom is actually an octagon.
Posted by: CRB | March 29, 2006 11:48 AM
Here is a graphic that shows the outline of the first triangle imposed over the second. The hypotenuse is not the same, and these are not triangles.
http://img209.imageshack.us/my.php?image=triangles21zg.gif
Posted by: JuryRig | March 29, 2006 02:25 PM
this is crap lol
Posted by: Anonymous | November 27, 2007 01:24 PM
It's kinda funny reading all this banter back and forth. We can't quite figure out why something so universally true seems to be untrue. We immediately compare this rediculous falshood to government officials and use it as a place to beat each other up about our beliefs. This puzzle is really quite simple... Look close, they give you a rectangular coordinate grid for a reason. If you look at the top right corner of the pink triangle in the second configuration (C2) and the same part of the entire triangle in the first configuration (C1) you'll notice that in that spot, C2 is actually taller than C1. This is also true directly above the "hole". What has happened here is that C2 is not a triangle at all since the "hypotenuse" of the large triangle is bowed outward so that the "hole" is distributed along the length of the "hypotenuse".
Posted by: Lookclose | March 16, 2008 10:48 PM
the big triangle isn't an enlargement of the smaller triangle, so the slope isn't a correct strraigt line. the picture beneath has a slight bump in it on the place where the two traingles touch
Posted by: hackzor | May 21, 2009 10:52 AM